TME 7 : Simulation logico-temporelle

Objectif

On souhaite réaliser dans ce TME un petit simulateur logico-temporel, permettant de simuler un réseau Booléen temporisé, où les expressions Booléennes sont représentées par des arbres EBM (voir TME3).

Les simulateurs à événements discrets permettent de simuler des systèmes matériels constitués d'un ensemble de composants matériels interconnectés par des signaux. Les signaux véhiculent fondamentatement deux tensions VSS et VDD représentant respectivement les valeurs Booléennes 0 et 1, mais le simulateur doit traiter plus de valeurs pour gérer les cas spéciaux comme les signaux en haute impédance, les conflits électriques, ou les valeurs indéfinies. A titre indicatif, le VHDL standard utilise 9 valeurs pour les signaux. Pour simplifier, nous nous limiterons dans ce TME aux trois valeurs logiques 0, 1, et U (indéfini).

Dans le cas général, Chaque composant est modélisé par un processus, et tous les processus s'exécutent en parallèle. Chaque processus utilise les valeurs de ses signaux d'entrées pour calculer les valeurs de ses signaux de sortie. Un signal possède un seul émetteur, mais peut avoir plusieurs destinataires. On définit, pour chaque processus, un sous-ensemble des signaux d'entrée, appelé liste de sensibilité du processus : un changement de valeur sur un signal appartenant à la liste de sensibilité peut entraîner un changement de valeur sur un signal de sortie du processus. Un processus doit donc être évalué à chaque fois que l'un des signaux de la liste de sensibilité change de valeur. Par exemple, la liste de sensibilité d'un processus représentant un automate de Moore ne comporte qu'un seul signal, qui est le signal d'horloge.

On s'intéresse dans ce TME au cas particulier des réseaux Booléens: un processus correspond à une expression Booléenne multi-niveaux. Dans ce cas particulier, un processus possède donc un seul signal de sortie, et la liste de sensibilité contient tous les signaux d'entrée. Cette liste de sensibilité est tout simplement le support de l'EBM, tel que vu au TME3. Le réseau Booléen peut être représenté par un graphe biparti comportant deux types de noeuds: des processus et des signaux. Les noeuds à la périphérie du réseau sont toujours des signaux.

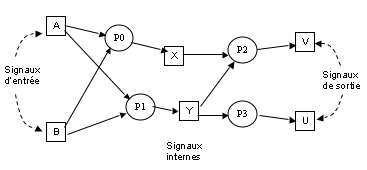
En d'autres termes, un processus a toujours au moins un signal entrant et un signal sortant. Les signaux qui n'ont pas d'arrête entrante sont les entrées primaires du réseau, les signaux qui n'ont pas d'arrête sortante sont les sorties primaires du réseau. Les autres signaux sont appelés signaux internes.

On appelle événement le changement de valeur d'un signal à un certain instant. Un événement est donc défini par un triplet (signal, date, valeur).

Simuler le fonctionnement d'un circuit consiste donc à calculer pour chaque signal la succession des événements, appelée forme d'onde. L'ensemble des formes d'ondes de tous les signaux constitue un chronogramme.

La simulation suppose que l'on possède une fonction d'évaluation qui calcule la valeur du signal de sortie du processus en fonction de la valeur des signaux d'entrée. Dans notre cas, nous utiliserons la méthode Ebm::eval() qui gère les trois valeurs de signaux (0,1,U).

Créez un répertoire de travail TME5, et copiez dans ce répertoire les fichiers qui se trouvent dans /users/enseig/jpc/M1-CAO/TME/5.public.

A) Structures de données

On utilise deux structures de données pour représenter :

• Le réseau Booléen (BoolNet), c'est à dire le graphe biparti des processus et des signaux.

• L'échéancier (Scheduler), c'est à dire l'ensemble ordonné des événements.

A1) réseau Booléen

Un réseau booléen est la représentation d'un graphe bipartie. Il est donc constitué de deux types de noeuds et d'arcs orientés reliants les noeuds entre eux.

Les deux types de noeuds sont les signaux et les processus.

Un arc orienté relie un noeud source à un noeud cible. Notez que comme le graphe est bipartie, les noeuds sources et destination sont toujours de types différents. On ne va pas créer d'objet spécifique pour représenter un arc. Plus simplement, les noeuds sources contiendront une liste de noeuds cible.

• Un Signal considéré comme source, peut être utilisé dans un nombre quelquonque de processus. il aura donc une liste de Processus cibles.

• Un processus considéré comme source aura une unique cible: le signal dont il calcule la valeur. Il n'est donc pas nécessaire de gérér une liste, un simple pointeur suffira. Notez qu'il s'agit d'une conséquence de notre simplification du modèle qui n'est pas applicable dans le cas général.

La classe BoolNet

En plus des accesseurs triviaux, elle fourni une fonction de recherche d'un signal par son nom getSignal(const std::string& ) ainsi que deux méthodes pour la construction du réseau booléen. Le réseau booléen est initialisé vide.

• Méthode addSignal(): ajoute un nouveau noeud de type signal. On donne le nom du signal ainsi que son type (parmis In, Out et Internal. La liste des cibles du noeud est initialisée vide.
• Méthode addProcess(): ajoute un nouveau noeud de type processus. On donne respectivement comme arguments, le nom du signal cible, l'expression booléenne qu'il représente (sous forme textuelle) et le delai de calcul de ce processus.

Importante remarque: la représentation des arcs (listes de cibles des noeuds sources) sont construites lors de la création des processus. Il est donc impératif que tous les signaux soient crées avant les processus.

class BoolNet {
  private:
    std::string            _name;
    std::vector<Signal*>   _signals;
    std::vector<Process*>  _processes;
  public:
                                  BoolNet      ( const std::string& );
    inline std::string&           getName      ();
           Signal*                getSignal    ( const std::string& );
    inline std::vector<Signal*>&  getSignals   ();
    inline std::vector<Process*>& getProcesses ();
           Signal*                addSignal    ( const std::string&, SignalType );
           Process*               addProcess   ( const std::string&, const std::string&, unsigned int delay );
           void                   toDot        ( std::ostream& );
           void                   toDot        ();
};

La classe Signal

Attributs:

• _network : le réseau booléen auquel elle appartient.
• _variable : l'EbmVar qu'elle encapsule. Le contructeur devra créer cette EbmVar à la contruction.
• _type : le type du signal (parmis In, Out et Internal).
• _processes : la représentation des arcs. On choisi un set<> pour gérer automatiquement l'unicité.

Méthode non triviale:

• addProcess() : ajoute une nouvelle cible à l'ensemble des cibles. Equivaut à créer un arc dans le graphe.
• toDot() : crée une représentation graphique du réseau booléen. Cette fonction vous est fournie.

class Signal {
  private:
    BoolNet*            _network;
    EbmVar*             _variable;
    SignalType          _type;
    std::set<Process*>  _processes;
  public:
                               Signal       ( BoolNet*, const std::string&, SignalType );
    inline std::string         getName      ();
    inline SignalType          getType      ();
    inline ValueType           getValue     ();
    inline std::set<Process*>& getProcesses ();
    inline void                addProcess   ( Process* );
    inline void                setValue     ( ValueType );
};

La classe Process

Attributs:

• _network : le réseau booléen auquel elle appartient.
• _signal : le signal qu'elle calcule. C'est la représentation de l'unique arc issu d'un noeud de type processus.
• _expression : l'EbmExpr de calcul. On la créera à l'aide de la méthode Ebm::parse() qui vous est fournie.
• _delay : le temps nécessaire au calcul de la nouvelle valeur. Représente un temps de propagation au travers des portes logiques.

Méthodes non triviales:

• Process() : le constructeur en plus de sa tâche d'initialisation des membres de l'objet devra créer les arcs entre les signaux appartenant au support de l'expression et le processus courant.
• eval() et display() sont des encapsulations des méthodes identiques de l'objet Ebm.

class Process {
  private:
    BoolNet*      _network;
    Signal*       _signal;
    Ebm*          _expression;
    unsigned int  _delay;
  public:
                         Process       ( BoolNet*, Signal*, const std::string& expression, unsigned int delay=0 );
           ValueType     eval          ();
    inline Ebm*          getExpression ();
    inline Signal*       getSignal     ();
    inline unsigned int  getDelay      ();
           void          display       ( std::ostream& );
           std::string   toString      ();
};

A2) échéancier

Le rôle de l'échéancier est d'enregistrer et d'ordonner les évènements dans le temps. Pour le réaliser nous avons besoin des éléments suivants:

• Une date (classe Time) contenant le temps écoulé depuis le début de la simulation en nano-secondes et un delta-cycle. Le delta-cycle permettant d'avoir plusieurs simulations au même temps physique mais cependant séparés pour ne pas générer de problèmes de causalité.

• Un événement (classe Event), comprtant le temps (Time) auquel il se produit, Le signal qu'il affecte et la nouvelle valeur que va prendre ce signal.

• Une structure lui permettant de stocker les ensembles d'évenements par dates et de trier ces ensembles par date (croissantes). Nous allons pour cela utiliser une map<> de vector<>. C'est à dire, une map<> dont chaque élément sera un vector<> d'évènements et la clé une date (Time). Notez qu'au sein d'un ensemble d'évènements synchrones l'ordre est indifférent.

Propriérés remarquables de la map<> de vector<>

Syntaxe:

map<Time, vector<Event*> >  _events;

La clé de tri est un objet de type Time et la valeur associée à cette clé un vector<Event*>. Il faudra définir pour la classe Time une surcharge de l'operateur strictement inférieur (operator<()) qui définira l'ordre chronologique.

Accès et itérateurs

map<Time, vector<Event*> >            _events;
map<Time, vector<Event*> >::iterator  istate = _events.begin();

for ( ; istate != _events.end() ; ++istate ) {
  const Time&     date   = (*istate).first;
  vector<Event*>& events = (*istate).second;

// Do something here.
}

• Ordre du parcours: une propriété fondamentale est que lors d'un parcours de la map<> avec des itérateurs, les éléments sont parcourus dans l'ordre défini par la relation d'ordre de la clé, c'est à dire dans notre cas, l'ordre chronologique de Time.

• Cet ordre est maintenu automatiquement lors d'ajout ou de retrait d'élements dans la map<>.

• Les itérateurs pointant sur des éléments de la map<> restent valides même si l'on ajoute ou retire des éléments (une seule exception: si l'on retire l'élement sur lequel l'itérateur pointe...).

• Les éléments d'une map<> sont des paires (clé,valeur), pour y accéder à partir de l'itérateur, il faut utiliser les attributs public first (clé) et second (valeur).

La classe Time

// Time is used as key by the scheduler's map<>.
class Time {
  private:
    unsigned int  _time;
    unsigned int  _deltaCycle;
  public:
    inline               Time          ( unsigned int time, unsigned int dc );
    inline unsigned int  getTime       () const;
    inline unsigned int  getDeltaCycle () const;
    friend bool          operator<     ( const Time& lhs, const Time& rhs );
};

La classe Event

L'attribut _value contient la prochaine valeur du signal. La méthode Event::updateSignalValue() est chargé de faire la mise à jour effective de la valeur du signal. Elle sera appelée dans l'étape de mise à jour du simulateur.

class Event {
  private:
    Signal*    _signal;
    ValueType  _value;
    Time       _time;
  public:
    inline             Event             ( Signal*, ValueType, Time& );
    inline  Signal*    getSignal         ();
    inline  ValueType  getValue          ();
    inline  Time&      getTime           ();
    inline  void       updateSignalValue ();
};

La classe Scheduler

Méthodes non triviales:

• addEvent(Signal*,...) : ajoute un nouvel évènement à l'échéancier. Pour donner la date on ne passe pas d'objet Time, mais ses deux composants time et dc.

• addEvent(const std::string&,...) : une surcharge de la fonction précédente qui prend comme premier argument un nom de signal au lieu du pointeur sur signal. Cette méthode sera utilisée préférentiellement pour initialiser l'échéancier.

• simulate() : effectue la simulation.

• toPatterns() : écrit dans le flot donné en argument le résultat de la simulation dans un format lisible par l'outil xpat. La définition de cette fonction vous est fournie.

• _reset() : remet toutes les variables (entrées, sorties, internes) à l'état initial (U).

• _header() et _display() : utilitaires vous permettant d'afficher l'état de la simulation à un instant donné.

class Scheduler {
  private:
    BoolNet*                              _network;
    std::map<Time, std::vector<Event*> >  _events;
  public:
           Scheduler  ( BoolNet* );
    Event* addEvent   ( const std::string& variable, ValueType, unsigned int time, unsigned int dc=0 );
    Event* addEvent   ( Signal*, ValueType, unsigned int time, unsigned int dc=0 );
    void   simulate   ();
    void   toPatterns ( std::ostream& );
    void   toPatterns ();
  private:
    void   _reset     ();
    void   _header    ();
    void   _display   ( const Time& );
};

C) Travail à réaliser

Dans un premier temps vous devrez utiliser le simulateur qui vous est fourni dans l'ensemble des fichiers .o.

Dans un second temps, il vous est demandé de progressivment remplacer les .o fournis par les vôtres.

C1) simulation du circuit And Or

Le fichier AndOr?.c contient un tout petit réseau Booléen ne contenant que deux noeuds, et 4 signaux. Compilez ce fihier, et exécutez la simulation.

Vous pouvez visualiser le réseau Booléen avec la commande:

> eog AndOr.png

Vous pouvez visualiser le chronogramme résulat de la simulation avec la commande:

> xpat -l AndOr

C2) Simulation d'un additionneur 2 bits

On se propose de simuler le schéma suivant, qui réalise un additionneur 2 bits. A chaque porte est associé une expression Booléenne représentée par un EBM.

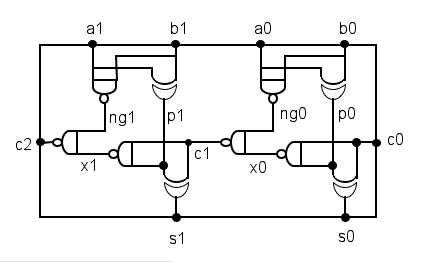
C2.1) Construction réseau Booléen de l'additionneur

En vous inspirant du fichier etou.c, écrivez le fichier Adder.c qui construit en mémoire le réseau Booléen correspondant au circuit additionneur 2 bits décrit ci-dessus. On utilisera pour cela les fonctions BoolNet::addProcess() et BoolNet::addSignal(). On prendra une valeur de 1 ns pour le temps de propagation de la porte NAND2, et de 2 ns pour la porte XOR2. Pour vérifier la structure du réseau Booléen, on utilisera la fonction toDot(). Cette fonction construit une représentation graphique du réseau Booléen, et la sauvegarde dans un fichier au format .gif ou .ps.

Modifiez le Makefile permettant de compiler ce programme Adder.c, et exécutez-le.

C2.2) Construction et initialisation de l’échéancier

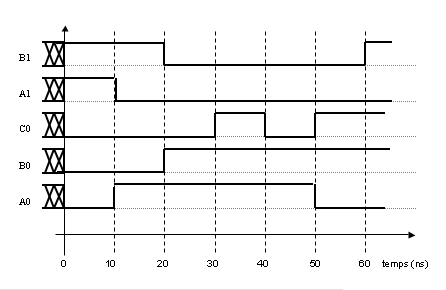
Compléter le fichier Adder.c main() pour créer l’échéancier et initialiser les événements sur les signaux d’ entrée a0, b0, c0, a1 et b1 de façon à respecter le chronogramme ci-dessous. On utilisera la fonction Scheduler::addEvent() et add_event(). Attention : le passage de la valeur U (indéfinie) à une valeur 0 ou 1 constitue un événement : Dans ce chronogramme, il y a donc un événement sur tous les signaux d’entrée au temps T = 0.

Pour vérifier que l’échéancier est correctement initialisé, on pourra utiliser la fonction Scheduler::drive(). Cette fonction peut être utilisée avant même l'exécution de la fonction de simulation, pour générer un fichier au format .pat qui décrit le chronogramme des signaux d'entrée. Vous pouvez visualiser ce chronogramme avec l’outil xpat.

C2.3) Simulation effective du circuit additionneur

Introduisez dans le fichier Adder.c la méthode Scheduler::simulate() qui effectue la simulation du réseau Booléen, jusqu'à ce qu'il n'y ait plus aucun événement à traiter dans l'échéancier. Compilez ce programme, et analysez le chronogramme résultant

C2.4) Ecriture de la boucle de simulation

Implémenter et remplacer progressivement toutes les classes qui vous on été fournies.