Error: Macro Include(TocTme) failed

pre-0.11 Wiki macro Include by provider <class 'includemacro.macros.IncludeMacro'> no longer supported

TME 8 : Méthode de partitionnement de graphe : Min-Cut

Objectif

On souhaite implanter en langage C un algorithme de partitionnement de graphe utilisant la méthode Min-Cut, dont le principe a été présenté en cours. Cet algorithme est fortement inspiré de la méthode publiée par Fiduccia et Mattheyses en 1982. Cet algorithme est souvent utilisé en CAO micro-électronique pour résoudre des problèmes de placement : Les noeuds du graphe représentent des cellules précaractérisèes à placer dans un plan, et l'existence d'une arête entre deux noeuds i et j représente l'existence d'une connection entre les deux deux cellules i et j.

A) Introduction

Soit un graphe G(N, H), où N est l'ensemble des noeuds, et H l'ensemble des arêtes. Une bipartition de G est formée de 2 sous-ensembles L (left) et R (right) de l'ensemble des noeuds N, dont l'intersection est vide, et l'union est égale à N.

En supposant que le nombre de noeud est pair, on dit qu'une bipartition est équilibrée si |L| = |R| = N/2

Dans le contexte du placement de cellules, on part d'une net-list de cellules précaractérisées, et on cherche à partitionner l'ensemble des cellules en deux sous-ensembles L et R tels que le nombre de signaux traversant la frontière entre les deux sous-ensembles soit minimal.

Nous allons raisonner sur un graphe non-orienté, défini de la façon suivante:

Les noeuds Ci représentent les cellules de la net-list (0 < i < N-1). Il existe une arête entre deux cellules Ci et Cj chaque fois qu'il existe au moins un signal connectant un port de la cellule Ci à un port de la cellule Cj.

Attention: avec cette définition, à un seul signal de la net-list peuvent correspondre plusieurs arêtes dans le graphe: si la sortie d'une cellule attaque n autres cellules, on a n arêtes dans le graphe.

On appelle «matrice d'adjacence» {Aij} la matrice carrée N * N qui représente la structure du graphe:

• Aij = 1 si il existe une arête dans le graphe entre les noeuds Ci et Cj
• Aij = 0 sinon

B) Algorithme MinCut glouton

On défini comme suit la fonction de coût du problème d'optimisation MinCut, dont la valeur dépend du nombre d'arcs qui traversent la frontière :

FC = 1/2 Somme  Aij * Kij
          i,j

Kij = 1 si les cellules Ci et Cj sont de part et d'autre de la frontière
Kij = 0 sinon

On part d'une bi-partition équilibrée initiale arbitraire en deux ensembles L et R, et on cherche à optimiser la fonction de coût FC, sans garantie d'atteindre le minimum absolu, mais avec un temps de calcul très court.

L'idée de base de l'algorithme est de pré-calculer, pour chaque cellule Ci un gain G(i) représentant la variation de la fonction de coût FC lorsqu'on déplace la cellule Ci d'un côté de la frontière à l'autre (sans déplacer aucune autre cellule).

Le gain G(i) est défini par:

G(i) = Somme  Aij * Dij
         j
Dij = +1 si les cellules Ci et Cj sont de part et d'autre de la frontière
Dij = -1  sinon

Après avoir calculé le gain G(i) pour toutes les cellules Ci, on classe les cellules dans deux listes ordonnées par gain décroissant (une liste ordonnée GAIN_L pour les cellules appartenant à L et une liste ordonnée GAIN_R pour les cellules appartenant à R).

Un mouvement élémentaire consiste à échanger deux cellules i et j :

• une cellule i appartenant à l'ensemble R passe dans l'ensemble L
• une cellule j appartenant à l'ensemble L passe dans l'ensemble R

La variation de la fonction de coût résultant du mouvement des cellules i et j peut être calculée de la façon suivante:

DFC(i<->j) = G(i) + G(j) - 2 * Aij

L'algorithme d'optimisation proposé est "glouton", car il n'y a pas de retour en arrière: Lorsqu'un mouvement a été accepté, les deux cellules déplacées i et j ne sont plus autorisées à bouger.

On considère la cellule i appartenant à R possédant le gain G(i) maximum, et la cellule j appartenant à L possédant le gain G(j) maximum. On calcule la variation de la fonction de coût associé à l'échange i <-> j, et on accepte le mouvement tant que celui-ci n'entraîne pas une augmentation de la fonction de coût.

C) Structures de données

On a besoin de deux structures de données séparées pour représenter d'une part le graphe à partitionner, et d'autre part les listes GAIN_L et GAIN_R. Cette seconde structure de donnée étant utilisée pour calculer les mouvements de cellules à effectuer, est appelée «gestionnaire de mouvements».

C1) représentation du graphe

Les noeuds du graphe sont identifiés par un index compris entre 0 et (NBNODE-1).

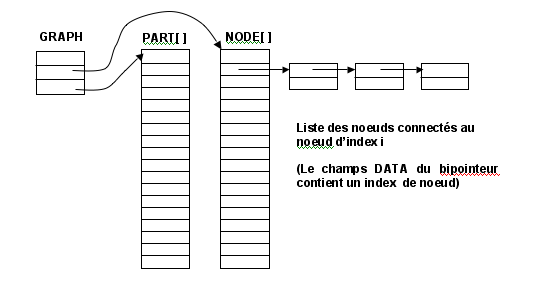
La structure du graphe est représentée par un tableau NODE[ ] indexé par le numéro du noeud (la taille du tableau est donc égale à NBNODE). Chaque case du tableau NODE[i] contient un pointeur sur une liste de bi-pointeurs représentant l'ensemble des noeuds adjacents au noeud [i]. Il y a donc un bipointeur pour chaque arête attachée au noeud[i].

Un second tableau PART[ ] est lui aussi indexé par le numéro du noeud. Chaque case PART[i] contient un entier définissant à quel sous-ensemble appartient le noeud [i]: (valeur 0 pour l'ensemble R, et valeur 1 pour l'ensemble L).

Le graphe est donc représenté par la structure suivante:

typedef struct graph_t {
  unsigned	NBNODE;	// nombre de noeuds du graphe
  bip_t	*	* NODE;	// pointeur sur le tableau NODE[NBNODE]
  unsigned	* PART;	// pointeur sur le tableau PART[NBNODE] 
} graph_t

C2) représentation du gestionnaire des mouvements

On appelle arité d'un noeud du graphe, le nombre d'arêtes attachées à ce noeud. Le gain maximum G(i) associé au mouvement d'un noeud [i] est au plus égal à l'arité du noeud [i]: Ce gain peut être positif ou négatif, mais sa valeur absolue ne peut pas être supérieure au nombre des noeuds auquel il est connecté. Soit GMAX la valeur maximale de l'arité (en considérant tous les noeuds du graphe). Pour tout noeud [i] du graphe, on a donc -GMAX < G(i) < GMAX

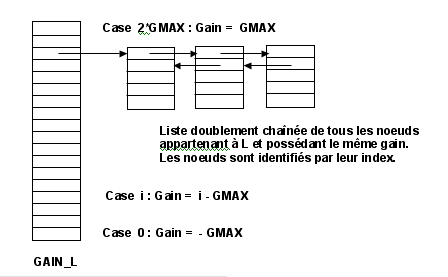
Pour représenter la liste ordonnée GAIN_L, on effectue une partition de l'ensemble des cellules appartenant à L, en regroupant dans un même sous ensemble tous les noeuds possédant le même gain. Ce sous ensemble est représenté par une liste doublement chaînée, dont chaque élément de type bichain_t contient un index de noeud. On définit un tableau de pointeurs GAIN_L[ ] possèdant 2 * GMAX + 1 cases, et indexé par une valeur de gain comprise entre -GMAX et GMAX. Chaque case correspond à une valeur de gain, et contient un pointeur sur une des listes doublement chaînées définies ci-dessus.

• Le gain des cellules rattachées à la case d'index 0 est égal à -GMAX
• Le gain des cellules rattachées à la case d'index i est égal à i - GMAX
• Le gain des cellules rattachées à la case d'index 2*GMAX est égal à GMAX

On fait la même chose pour représenter la liste GAIN_R.

Au début de l'algorithme, chaque noeud du graphe est inséré dans la liste chaînée qui correspond à sa valeur de gain. Au fur et à mesure que les noeuds sont transférés, les listes se vident, car un noeud qui a subi un mouvement n'est plus autorisé à bouger. Puisque le gain des noeuds change au cours de l'algorithme, un même noeud peut être retiré d'une liste et inséré dans une autre, ce qui justifie l'utilisation de listes doublement chaînées.

Dans la structure de donnée «graphe_t» représentant le graphe, les noeuds du graphe sont identifiés par leur index. On a donc besoin d'introduire dans la structure «move_manager_t» représentant le gestionnaire de mouvements, un moyen d'obtenir le pointeur sur la structure bichain_t représentant un noeud du graphe lorsqu'on connait son index. On construit donc un tableau de pointeurs NODES [ ], indexé par le numéro du noeud. On utilise donc les structures suivantes:

typedef struct bichain_t {
  bichain_t	*NEXT;	// pointeur sur le noeud suivant de même gain
  bichain_t	*PREV;	// pointeur sur le noeud précédent de même gain
  unsigned	INODE;	// index du noeud
  int		IGAIN;  // index dans le tableau des gains 
  unsigned  PART;       // numero de la partie 0 pour R, 1 pour L
} bichain_t

typedef struct move_manager_t {
  int	    GMAX;	    // la taille des tableaux GAIN_R et GAIN_L est égale à 2*GMAX+1
  bichain_t **GAIN_L;	// pointeur sur le tableau de pointeurs pour la partie gauche
  bichain_t **GAIN_R;	// pointeur sur le tableau de pointeurs  pour la partie droite
  int	    LX;		// index de la première case non vide de GAIN_L (init à -1)
  int	    RX;		// index de la première case non vide de GAIN_R (init à -1)
  bichain_t **NODES;	// pointeur sur le tableau de pointeurs sur les noeuds 
} move_manager_t

D) Fonctions d'accès aux structures de données

On dispose d'un ensemble de fonctions permettant de construire et de manipuler les deux structures de données graph_t et move_manager_t.

graph_t * parse_graph(char *filename)

Cette fonction prend pour argument un nom de fichier au format .dot représentant le graphe à partitionner, construit en mémoire la structure graph_t correspondante, et renvoie un pointeur sur cette structure. Si aucune partition initiale n'est définie dans le fichier .dot, les noeuds d'index inférieur à NBNODE/2 sont arbitrairement rangés dans le sous-ensemble L, et les noeuds d'index supérieur à NBNODE/2 sont rangés dans le sous-ensemble R.

Un exemple de fichier au format .dot est donné ci-dessous. Les noeuds du graphe sont identifiés par un index, il y a une ligne par arête, les deux sous-graphes cluster0 et cluster1 définissent la partition initiale et sont optionnels.

graph
{
  // la définition des clusters est optionnelle
  subgraph cluster0 {0 1 2 3} 
  subgraph cluster1 {4 5 6 7}
  0--4
  0--5
  0--7
  1--5
  3--7
  1--2
  5--6
}

void drive_graph(graph_t *p, char *filename)

Cette fonction prend pour argument un pointeur p sur une structure graph_t, ainsi que le nom du fichier de sortie, et écrit sur disque un fichier au format .dot, en conservant dans le fichier les informations de partition (sous-ensemble L et R). Ce format est affichable sous forme graphique et permet de visualiser la partition.

bichain_t * cons_bichain (bichain_t *prev, bichain_t *next, unsigned inode, int igain, unsigned part)

Cette fonction alloue la mémoire nécessaire pour créer un objet de type bichain_t appartenant à une liste doublement chaînée, elle initialise les différents champs de cette structure, et renvoie un pointeur sur cette structure.

void free_bichain (bichain_t *p)

Cette fonction libère la mémoire allouée lors de la construction de l'objet bichain_t par la donction cons_bichain().

move_manager_t * cons_move_manager(graph_t *p)

Cette fonction pend pour argument un pointeur sur la structure représentant le graphe partitionné, et construit en mémoire la structure move_manager_t correspondant à cette partition.

void add_node (move_manager_t *mm, bichain_t *node)

Cette fonction prend pour arguments un pointeur sur la structure représentant le gestionnaire de mouvements et un pointeur sur un élément de type bichain_t représentant un noeud) dont les champs INODE, IGAIN et PART sont définis. Elle range ce noeud dans la liste doublement chaînée correspondante, elle met à jour le tableau NODES et les index LX ou LR. Les champs NEXT et PREV sont initialisés par la fonction add_node().

bichain_t * del_node(move_manager_t *mm, bichain_t *node)

cette fonction prend pour arguments un pointeur sur la structure représentant le gestionnaire de mouvements, et un pointeur sur un élément de liste doublement chaînée (représentant un noeud). Elle retire cet élément de la liste doublement chaînée, met à jour le chaînage et les index LX et RX, enfin renvoie un pointeur sur la structure bichain_t pour une éventuelle libération de la mémoire.

int compute_gain (graph_t *g, unsigned index)

Cette fonction prend pour argument un pointeur sur la structure représentant le graphe, un index désignant un noeud particulier, et calcule le gain associé à ce noeud, pour la partition courante.

int global_cost (graph_t *g)

Cette fonction prend pour argument un pointeur sur la structure représentant le graphe, calcule la fonction de coût globale pour la partition courante, et renvoie la valeur calculée.

E) Travail à réaliser

Créez un répertoire de travail tme8, et copiez dans ce répertoire tous les fichiers et répertoires qui se trouvent dans

/users/enseig/encadr/cao/tme8

Dans un premier temps vous devez utiliser les fonctions qui vous sont fournies pour écrire le programme main() qui effectue le partitionnement d'un graphe quelconque défini dans un fichier au format .dot. Dans un deuxième temps vous devrez programmer vous même les différentes fonctions et remplacer progressivement les fichiers objets fournis par vos propres fichiers objet.

1. Construction et initialisation du gestionnaire de mouvements

Ecrivez le programme main() qui construit en mémoire les deux structures de données graph_t et move_manager_t. Vous disposez pour vous aidez d'une fonction dump_move_manager() qui affiche le contenu de la structure.

2. Exécution et évaluation

Complétez le programme main() en ajoutant la fonction mincut(graph_t *gr, move_manager_t *mm). On utilisera la fonction global_cost(graph_t *g) pour calculer et afficher le coût de la partition avant et après optimisation. Exécutez cet algorithme sur différents graphes que vous définirez vous-mêmes. La partition résultante est-elle toujours la partition optimale? Pourquoi? Donnez un contre-exemple.

3. Ecriture de la fonction mincut()

Ecrire en langage C la fonction mincut() qui réalise l'algorithme MinCut glouton. Cette fonction contient la boucle réalisant les transferts de cellules tant que le transfert fait décroitre la fonction de coût. A chaque tour dans cette boucle, une cellule du sous-ensemble L passe dans R, et une cellule du sous-ensemble R passe dans L. Les deux cellules i et j qui on bougé doivent être retirées de la structure de donnée move_manager, et les gains de toutes les cellules adjacentes à i et j doivent être mis à jour.

4. Ecriture des autres fonctions d'accès

Ecrire les différentes fonctions d'accès aux structures de données définies dans la partie D, et validez ces fonctions en les intégrant peu à peu dans votre programme.

5. construction du graphe en mémoire

L'objectif est ici d'écrire la fonction parse_graph(), en utilisant lex et yacc. Nous vous suggérons de commencer par faire l'hypothèse qu'il n'y a pas de clusters dans le fichier, puis d'introduire les clusters dans la grammaire de ce petit langage.

Compte-Rendu

Il ne vous est pas demandé de compte-rendu écrit pour ce TME, mais vous devrez faire une démonstration de votre code au début du prochain TME.