Problème 1023
Dans la première multiplication (en bleu), tous les chiffres, représentés par des « ? » sont premiers (ils ne peuvent être que 2, 3, 5 ou 7).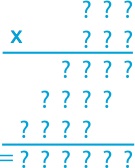
- 1A, 1B, 1C. Écrivez son résultat.
Dans la deuxième multiplication (en orange), les « A » représentent des chiffres impairs (1, 3, 5, 7 ou 9), les « G » des chiffres pairs (0, 2, 4, 6 ou 8).
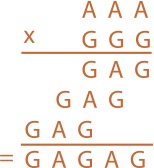
- 2A, 2B, 2C. Écrivez son résultat.
Pour chaque question, s'il n'y a qu'une réponse, la mettre dans la case A. S'il y en a plusieurs, les écrire dans l'ordre croissant à partir de la gauche, en s'arrêtant à la colonne C, même s'il y a plus de trois réponses possibles.
Pour ce problème, une énumération exhaustive ne pose pas de problème. La seule subtilité consiste à vérifier le nombre de chiffres des différents résultats (intermédiaires et finaux). Afin de pouvoir faire l'exploration, il faut également convertir un tableau d'entiers en un seul entier ([1, 2] → 12) et inversement.
Le code est disponible ici.
Le code est disponible ici.
- 1A. 252 525.
- 2A. 29 036