Problème 1066
Chacune des 45 cases de cette enseigne de pharmacie contient une lampe qui s’allume en vert.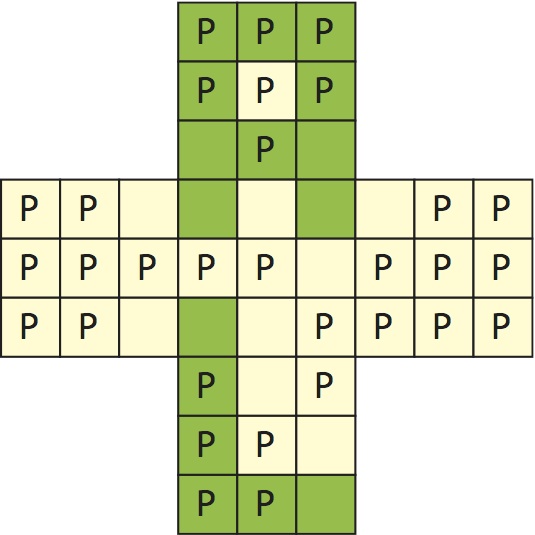
Le pharmacien, facétieux et pingre, allume seulement certaines des lampes (au moins une), puis compte pour chaque case combien de cases adjacentes (par un côté) sont allumées. Quand c’est un nombre pair, il annonce que la case est « pépère ». Par exemple, ci-dessus, 16 lampes sont allumées et 31 cases (marquées P) sont pépères.
Le mardi, le pharmacien crée un maximum de cases pépères, le jeudi, il en crée un minimum.
- 1. Combien de lampes, au moins, doit-il allumer le mardi ? (5 points)
- 2. Combien de lampes, au moins, doit-il allumer le jeudi ? (5 points)
Pour ce problème, une énumération exhaustive de toutes les configurations de lampes allumées/non-allumées n'est pas envisageable en temps raisonnable (plusieurs semaines/mois). De plus, il y a deux problèmes en un : d'une part, il faut trouver le nombre minimal atteignable de cases P ; d'autre part, il faut trouver le nombre minimal de lampes à allumer pour atteindre ce minimum.
Ainsi, l'idée pour avoir un temps d'exploration raisonnable est de compter le nombre de cases P au fur et à mesure de l'exploration, et de ne fixer la valeur d'une case que si le nombre de cases P courant plus celui créé par cette nouvelle valeur fixée ne dépasse pas le minimum déjà atteint. Cela est possible du fait de l'ordre de parcours des cases (de gauche à droite, de haut en bas) : quand on fixe la valeur d'une case donnée, la case se trouvant au-dessus aura tous ses voisins déterminés, et son nature P ou non définie (en réalité, la condition est un peu plus compliquée que ça à cause de la forme de croix). De cette manière, l'exploration avec affichage prend 3 centièmes de secondes en -O0.
Le code est disponible ici.
Ainsi, l'idée pour avoir un temps d'exploration raisonnable est de compter le nombre de cases P au fur et à mesure de l'exploration, et de ne fixer la valeur d'une case que si le nombre de cases P courant plus celui créé par cette nouvelle valeur fixée ne dépasse pas le minimum déjà atteint. Cela est possible du fait de l'ordre de parcours des cases (de gauche à droite, de haut en bas) : quand on fixe la valeur d'une case donnée, la case se trouvant au-dessus aura tous ses voisins déterminés, et son nature P ou non définie (en réalité, la condition est un peu plus compliquée que ça à cause de la forme de croix). De cette manière, l'exploration avec affichage prend 3 centièmes de secondes en -O0.
Le code est disponible ici.
- 1. 6
- 2. 16