Problem 1066
Each of the 45 cells in this pharmacy sign contains a lamp that lights green.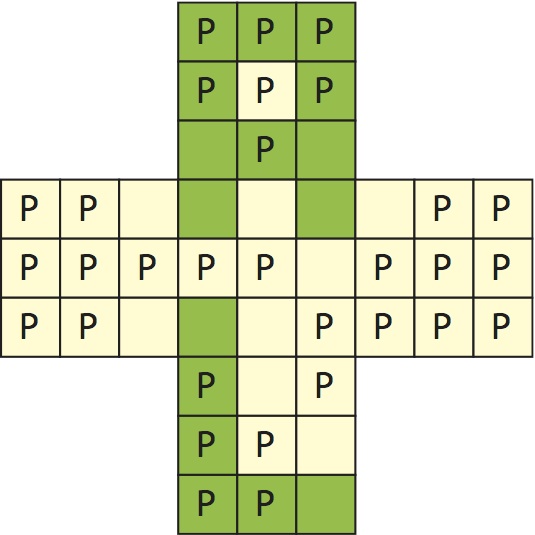
The pharmacist, facetious and stingy, turns on only some of the lamps (at least one), then counts for each cell how many adjacent cells (on one side) are lit. When it is an even number, he announces that the cell is "cushy". For example, above, 16 lamps are lit and 31 cells (marked P) are cushy.
On Tuesday, the pharmacist creates a maximum of cushy cells, on Thursday, he creates a minimum.
- 1. How many lamps, at least, should he turn on Tuesday? (5 points)
- 2. How many lamps, at least, should he turn on Thursday? (5 points)
For this problem, an exhaustive enumeration of all the configurations of lit/unlit lamps is not possible in reasonable time (several weeks/month). Moreover, there are two problems in one: on the one hand, it is necessary to find the minimum attainable number of P cells; on the other hand, it is necessary to find the minimum number of lamps to light to reach this minimum.
Thus, the idea for having a reasonable exploration time is to count the number of P cells as the exploration progresses, and to set the value of a cell only if the number of current P cells plus the one created by this new fixed value does not exceed the minimum already reached. This is possible because of the order in which the cells are set in the enumeration (from left to right, from top to bottom): when the value of a given cell is set, the cell above will have all its neighbors determined, and its nature (P or not) as well (in reality, the condition is a little more complicated than that because of the shape of the cross). In this way, the execution with display takes 3 hundredths of a second in -O0.
The code is available here.
Thus, the idea for having a reasonable exploration time is to count the number of P cells as the exploration progresses, and to set the value of a cell only if the number of current P cells plus the one created by this new fixed value does not exceed the minimum already reached. This is possible because of the order in which the cells are set in the enumeration (from left to right, from top to bottom): when the value of a given cell is set, the cell above will have all its neighbors determined, and its nature (P or not) as well (in reality, the condition is a little more complicated than that because of the shape of the cross). In this way, the execution with display takes 3 hundredths of a second in -O0.
The code is available here.
- 1. 6
- 2. 16