Problème 1070
Cinq pièces de monnaie sont placées (position de gauche) sur cinq cases de la grille 3 × 3 ci-dessous.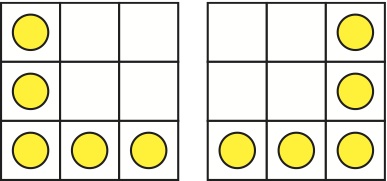
Lors de chaque « coup », une des pièces a le droit de courir vers une case libre (sans aucune condition de placement entre la case de départ et la case d'arrivée) , à condition que cette case ait un côté commun avec exactement deux cases contenant déjà chacune une (autre) pièce.
- 1. En combien de coups, au minimum, peut-on atteindre la position de droite ? (8 points) (répondre 0 si c’est impossible)
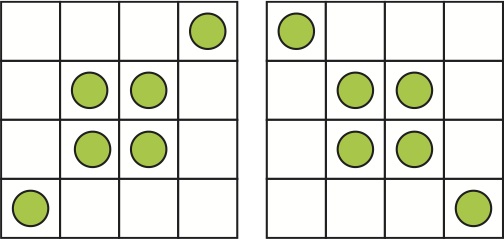
- 2. Même question pour passer de la position de gauche à la position de droite pour les six pièces de la grille 4 × 4 ci-dessous. (8 points)
Pour ce problème, l'idée est de faire une exploration en largeur de toutes les configurations atteignables à partir de la configuration initiale (par nombre de coups croissants). Une difficulté de ce programme est de pouvoir avoir obtenir la trace arrière, de la configuration finale à la configuration initiale (pour pouvoir obtenir la liste des coups à effectuer). Cela exige notamment d'implémenter la validité des coups arrière et de stocker la profondeur des coups.
Pour le reste : une configuration est encodée sur un entier, et l'ensemble des configurations déjà explorées est stocké dans une structure arborescente indexée par la valeur de case correspondant à la profondeur courante. Enfin, comme les cases de destination possible sont indépendantes des cases de départ, elles peuvent être calculées une seule fois pour une configuration à explorer, avant de tester chaque mouvement possible (il faut quand même tenir compte du fait que la case courante soit adjacente, auquel cas celle-ci ne doit pas être comptée).
Le code est disponible ici. Par ailleurs, étant donnée la combinatoire (notamment pour la question 2), je ne sais pas comment ont fait les personnes qui ont répondu correctement à cette question sans faire de programme...
Pour le reste : une configuration est encodée sur un entier, et l'ensemble des configurations déjà explorées est stocké dans une structure arborescente indexée par la valeur de case correspondant à la profondeur courante. Enfin, comme les cases de destination possible sont indépendantes des cases de départ, elles peuvent être calculées une seule fois pour une configuration à explorer, avant de tester chaque mouvement possible (il faut quand même tenir compte du fait que la case courante soit adjacente, auquel cas celle-ci ne doit pas être comptée).
Le code est disponible ici. Par ailleurs, étant donnée la combinatoire (notamment pour la question 2), je ne sais pas comment ont fait les personnes qui ont répondu correctement à cette question sans faire de programme...
- 1. 8
- 2. 18