Problem 1070
Five coins are placed (left position) on five boxes of the grid 3 × 3 below.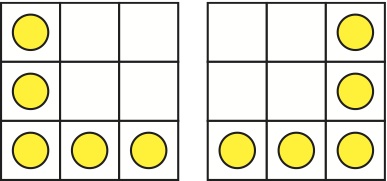
At each « move », one of the coins is moved into one of the free squares (with no restriction on the location of the target square w.r.t. the source square), to the condition that the target square has a side in common with exactly two squares containing already another coin.
- 1. In how many moves, at least, can we reach the right position? (8 points) (answer 0 if it is impossible)
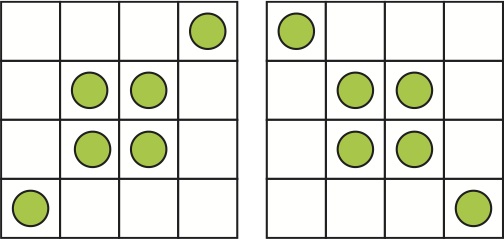
- 2. Same question to go from the left position to the right position for the six coins in the 4 × 4 grid below. (8 points)
For this problem, the idea is to make a breadth-first exploration of all the configurations that can be reached from the initial configuration (by increasing number of moves). A difficulty of this program is to be able to backtrace from the final configuration to the initial configuration (in order to get all the moves to take). This requires, in particular, to implement the validity of the inverse of moves, and to store the depth of the moves.
For the rest: a configuration is encoded on an integer, and the set of configurations already explored is stored in a tree structure indexed by the cell value corresponding to the current depth. Finally, since the possible destination cells are independent of the starting cell, they can be calculated only once for a configuration to be explored, before testing each possible move (we must nevertheless take into account the fact that the current cell is adjacent or not, in which case it should not be counted as a neighbour).
The code is available here.
For the rest: a configuration is encoded on an integer, and the set of configurations already explored is stored in a tree structure indexed by the cell value corresponding to the current depth. Finally, since the possible destination cells are independent of the starting cell, they can be calculated only once for a configuration to be explored, before testing each possible move (we must nevertheless take into account the fact that the current cell is adjacent or not, in which case it should not be counted as a neighbour).
The code is available here.
- 1. 8
- 2. 18