INDEX

DOCS → [Config] [MIPS U] [MIPS K] [​markdown] [CR.md]
COURS → [1 (+code) (+outils)] [2] [3] [4] [5] [6] [7] [8] [9]
TME → [1] [2] [3] [4] [5] [6] [7] [8] [9]
CODE → [gcc + soc] [1] [2] [3] [4] [5] [6] [7] [8] [9]

4 - Cache L1 à correspondance directe - performance

Vous pouvez lire les slides de cours pour voir les détails, mais voici le résumé des principes en quelques lignes.

Les caches L1 ont pour but d'améliorer les performances en réduisant le nombre de cycles nécessaires pour accéder à la mémoire à la fois pour les instructions que pour les données. Le tampon d'écriture, présent dans le cache mais qui n'est pas un cache, permet aussi de réduire la latence des écritures de données (elle est même nulle la plupart du temps).

On cherche à évaluer l'influence des mémoires caches sur les performances du système. Pour évaluer la performance, on utilise comme mesure le nombre moyen de Cycles Par Instruction (CPI).

Dans un système mémoire parfait, le taux de HIT est de 100% sur le cache d'instructions comme sur le cache de données : c'est-à-dire que toutes les requêtes de lecture du processeur vers la mémoire sont satisfaites immédiatement. Mais dans un système mémoire réel, la capacité de stockage limitée des caches (cache d'instructions et cache de données) a pour effet de dégrader la performance : certaines requêtes de lecture font MISS (échec de cache), et le processeur est gelé pendant plusieurs cycles en attendant que la ligne de cache manquante soit lue en mémoire par le contrôleur du cache. Ces cycles de gel du processeur augmentent évidemment la valeur du nombre moyen de cycles par instruction (CPI).

Cette augmentation du CPI dépend évidemment du taux de MISS (proportion de requêtes du processeur qui font MISS), mais dépend également du coût du MISS (nombre moyen de cycles de gel pour rapatrier la ligne de cache manquante en cas de gel). En cas de MISS sur un cache L1, cache de 1^er niveau, le nombre de cycles de gel peut être très élevé (plusieurs centaines de cycles), s'il faut aller chercher la ligne de cache dans la mémoire externe. Le cache L2, ou cache de 2^ème niveau, joue le rôle d'un "accélérateur", qui permet de limiter le coût du MISS. Dans tous les calculs de cette séance, nous allons raisonner sur des valeurs moyennes.

Note : ces valeurs moyennes dépendent évidemment des programmes exécutés, et les valeurs proposées ci-dessous sont fournies à titre d'exemple.

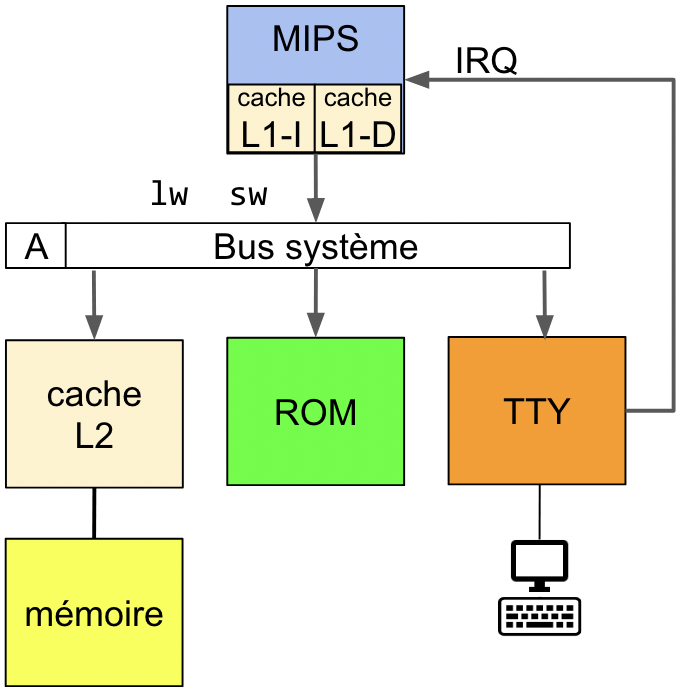
Comme illustré dans le schéma à droite, on s'intéresse à une plateforme matérielle comportant un processeur MIPS32, possédant deux caches L1 séparés, pour les instructions et pour les données. Le cache de données suit une politique d'écriture write through (toute requête d'écriture provenant du processeur est enregistrée dans un tampon d'écritures postées, puis transmise vers la mémoire). Compte tenu de la taille des caches L1 et des applications exécutées, on observe que le taux de MISS moyen est de 4% sur le cache L1 d'instructions et de 8% sur le cache L1 des données.

En cas de MISS sur un cache L1, le contrôleur du cache L1 s'adresse au cache L2, par l'intermédiaire d'un bus système de largeur 32 bits. On suppose que le processeur, les 2 caches L1, la ROM de démarrage, le bus système et le cache L2 sont intégrés sur la même puce, et fonctionnent à la même fréquence d'horloge. La largeur d'une ligne de cache est de 16 octets (soit 4 mots de 32 bits). En cas de MISS sur le cache L2, le contrôleur du cache L2 doit chercher la ligne de cache manquante dans la mémoire principale, qui est une mémoire externe à la puce.

A. Questions de cours

1. Que signifie « taux de MISS » ? De quoi dépend-il ? Est-il stable ? Quelle est sa valeur typique ?
2. Qu'est-ce que le coût d'un MISS ? De quoi dépend-il ? Quelle est sa valeur typique ?
3. Que signifient CPI et IPC ? Quel est le rapport entre les deux ?
4. Sur un processeur capable de démarrer une instruction par cycle, pourquoi on n'a pas un CPI de 1 ?
5. Finalement, quelle est l'équation définissant le CPI réel en fonction du CPI0 (avec un cache parfait, donc un taux de MISS de 0%) et de taux de MISS réel et des coûts de MISS ?
6. Qu'est-ce qu'une perte de cohérence pour un cache de niveau 1 ? Est-ce grave ?
7. Est-ce qu'il y a un risque de perte de cohérence si on a un seul processeur ? Et s'il y en a plus qu'un ?
8. Un moyen d'éviter le problème de cohérence, c'est le snooping, qu'est-ce que c'est ?
9. Quels autres moyens connaissez-vous pour traiter le problème de cohérence ?
10. Qu'est-ce qu'un faux partage ? (Non, ce n'est pas quand votre petit frère coupe un gâteau pour vous en donner une part)
11. Est-ce que le faux partage est un problème grave ?

B. Influence des mémoires cache sur les performances

B.1. Système mémoire parfait

On suppose que, pour le programme exécuté, on a mesuré les fréquences suivantes pour les différents types d'instruction exécutées par le processeur MIPS32 :

• opérations entre registres : 55%
• branchements : 25%
• lecture de données : 10%
• écriture de données : 10%

Le processeur MIPS32 de la plateforme est un processeur RISC à architecture pipe-line. Il est donc capable de démarrer l'exécution d'une instruction à chaque cycle, ce qui correspond en principe à un CPI de 1 cycle/instruction. Malheureusement, même avec un système mémoire parfait (pas de MISS sur les caches), la valeur du CPI est supérieure à 1, car certaines instructions ont une durée supérieure à un cycle :

• lorsque le processeur exécute une instruction de branchement, la durée effective de l'instruction est de 2 cycles au lieu de 1 cycle, que le branchement réussisse ou non.
• lorsqu'une instruction de lecture de donnée en mémoire est suivie par une instruction qui utilise la donnée lue par la première (on dit qu'il y a une dépendance de donnée entre les 2 instructions), la durée effective de l'instruction de lecture est de 2 cycles au lieu de 1 cycle. Notez que le compilateur le sait et il évite ces cas quand c'est possible.

1. Calculez la valeur CPI0 (correspondant à un système mémoire parfait) en supposant que 50% des instructions de lecture de donnée sont en dépendance avec l'instruction suivante ? (Il faut faire une somme des durées pondérées par leur taux d'occurence)
2. Quel est le pourcentage de gel dans les conditions précédentes avec un système mémoire parfait.

B.2. Estimation du coût du MISS

Lorsqu'une requête de lecture du processeur fait MISS sur l'un des deux caches L1 alors le processeur est gelé. Le contrôleur du cache L1 doit, dans ce cas, effectuer une transaction sur le bus système pour accéder au cache L2 afin de récupérer la ligne manquante. Le temps nécessaire à récupérer la ligne manquante définit le coût d'un MISS. Voyons qu'elles sont les étapes:

1. Le cache L1 doit déclencher une lecture sur le bus système → disons : 4 cycles
   (cela dépend du temps que met l'arbitre du bus pour autoriser la transaction)
2. Le cache L2 doit lire la ligne → 20 cycles
   (c'est un cache, il faut tenir compte qu'il peut aussi faire MISS)
3. La ligne doit être transférée sur le bus entre le cache L2 et le cache L1 → 4 cycles
   (cette durée dépend de la longueur de la ligne, plus elle est longue, plus le nombre de cycles est grand)
4. Le cache L1 doit mettre à jour la case recevant la ligne → 2 cycles
   (la mise à jour du répertoire et le dégel du processeur, c'est ce que l'on a observé dans le simulateur, dans le TP précédent)

En tenant compte des hypothèses précédentes, le coût moyen d'un MISS sur le cache L1 est donc de 30 cycles (c'est un ordre de grandeur). On cherche à évaluer l'augmentation du CPI causée par les MISS sur le cache d'instructions. On note DCPI_ins cet accroissement. Puis à évaluer l'augmentation du CPI causée par les MISS sur le cache de données. On note DCPI_data cet accroissement.

1. Calculez la valeur de DCPI_ins, donc l'accroissement du CPI dû au cache instruction, en utilisant le taux de MISS défini dans l'énoncé (4%), et le coût du MISS (30 cycles).
   Aide : 100% des instructions entraînent une lecture du cache instruction
2. Calculez la valeur de DCPI_data, donc l'accroissement du CPI dû au cache data, en utilisant le taux de MISS défini dans l'énoncé (8%) et le coût du MISS de 30 cycles.
   Aide : seules 10% des instructions entraînent une lecture du cache data.
3. Sachant que 10% des instructions sont des écritures, expliquez pourquoi les écritures n'entraînent pas d'augmentation directe du CPI, bien que toute écriture entraîne un accès au bus système (politique write through) ?
4. Faut-il traiter comme un cas particulier les situations où le processeur émet simultanément (i.e. au même cycle) des requêtes d'instructions et de données qui font à la fois MISS sur le cache d'instructions et MISS sur le cache de données ?
   On suppose un processeur pipeliné
5. Quelle est finalement la valeur du nombre moyen de cycles par instruction ?
6. Calculez la valeur du CPI lorsqu'on désactive les caches L1. Que se passe-t-il si on désactive aussi le cache L2 et que la durée d'accès est disons 400 cycles ?

C. Travaux pratiques

Le but de ce second TP sur les caches est de vérifier expérimentalement l'évolution de la performance du processeur (mesurée en CPI) en fonction de la taille des caches. Vous allez faire varier les capacités des caches L1 instructions et données, et vous allez mesurer la durée d'exécution d'une application logicielle un peu plus complexe que celle du précédent TP. La largeur des lignes des deux caches est fixée à 16 octets (soit 4 mots). Vous ferez donc varier la capacité des deux caches en faisant varier uniquement le nombre de cases.

Commencez par recopier le tp4 dans votre répertoire de travail, sont le contenu est (vous savez où est l'archive) :

tp4
├── Makefile
└── src
    ├── harch.c
    ├── harch.h
    ├── hcpu.S
    ├── hcpu.h
    ├── jpeg.h
    ├── kernel.ld
    ├── kinit.c
    ├── klibc.c
    └── klibc.h

Ce répertoire tp4 contient 1 répertoire, il y a tous les fichiers nécessaires à la génération du code binaire kernel.x, dont un fichier Makefile permettant de le générer automatiquement. Comme pour le précédent TP, ces fichiers représentent une version minimaliste du système (vu au tp1), il n'y a presque rien, mais le but est d'analyser le comportement des caches, donc moins il y a de code à exécuter avant la fonction que vous allez analyser, mieux c'est.

L'application logicielle proposée pour ce TP effectue un calcul de traitement d'image appelé transformation cosinus inverse (IDCT). Cette transformation est une variante de la transformée de Fourier à deux dimensions. L'application traite une image en découpant cette image en blocs de (8 * 8) pixels. Elle est écrite en langage C, et vous pouvez trouver son contenu dans le fichier kinit.c. Il n'est pas nécessaire de comprendre l'algorithme IDCT pour faire ce TP.

Comme vous l'avez appris au TP précédent :

• le simulateur almo1.x permet de faire varier le nombre de cases des caches L1, grâce à deux arguments à passer sur la ligne de commande. On peut aussi faire varier la longueur des lignes mais ce ne sera pas le cas dans ce TP. Attention : les valeurs que l'on peut donner pour ces arguments doivent être des puissances de 2 :
  • -NICACHESET spécifie le nombre de cases du cache d'instructions,
  • -NDCACHESET spécifie le nombre de cases du cache de données.

• En outre, en utilisant l'argument -STATS pour le simulateur, vous pouvez obtenir les statistiques sur les taux de MISS des caches et le CPI. La commande make cachestats NICACHESET=1 NDCACHESET=1 lance de simulateur avec les caches instructions et données de 1 case, et le simulateur génère le fichier stats.txt contenant les informations statistiques listées ci-après. Ces informations sont fabriquées à partir de compteurs dans la plateforme, relevés tous les 10 cycles qui caractérisent l'activité des caches.
  Chaque ligne de ce fichier de stats.txt contient 8 valeurs :
  
  
  1. Le nombre de cycles simulés depuis le démarrage de la machine (incrément de 10),
  2. Le nombre d'instructions exécutées depuis le démarrage de la machine,
  3. Le nombre de MISS sur le cache d'instructions depuis le démarrage de la machine,
  4. Le nombre de lectures de données depuis le démarrage de la machine,
  5. Le nombre de MISS sur le cache de données depuis le démarrage de la machine,
  6. Le taux de MISS sur le cache d'instructions,
  7. Le taux de MISS sur le cache de données,
  8. Le CPI, qui est le nombre moyen de cycles par instruction.

Une chose nouvelle sur le simulateur.

• Le simulateur almo1.x permet de rediriger la sortie texte vers un fichier plutôt que de l'afficher sur le terminal TTY, comme habituellement). Pour cela, avant de lancer la simulation avec make, il faut entrer la commande shell suivante :

  $ export SOCLIB_TTY=FILES
  

• Pour revenir à l'affichage dans une fenêtre TTY, taper la commande shell :

  $ export SOCLIB_TTY=TTY
  

Si vous avez envie de vous challenger, vous pouvez modifier le fichier Makefile pour intégrer cette option. Vous pourriez avoir par défaut une utilisation des fenêtres TTY et, de manière optionnelle, une utilisation des fichiers. Ce n'est pas très difficile, mais ça vous oblige à lire le Makefile (il y a une ligne dans le fichier à ajouter et une à modifier, c'est tout).

• Vous auriez par exemple:

  $ make exec                 → utilise xterms
  $ make exec TTY=FILES       → utilise les fichiers 
  

C.1. Caches de faible capacité

Vous allez compiler le code et lancez le simulateur avec des caches L1 (instructions et données) dont la capacité est d'une seule case avec la génération des statistiques. Chaque cache a donc une capacité de 16 octets.
Lancez le simulateur avec des caches d'1 case

make cachestats NICACHESET=1 NDCACHESET=1

1. Quel est le CPI (nombre moyen de Cycles Par Instruction) pour ces tailles de cache ?

make exec NICACHESET=1 NDCACHESET=1

2. Quel est le temps d'exécution de l'application (en nombre de cycles) ?

Relancez la simulation en doublant la capacité des caches à 32 octets (2 cases). Attention : pour ne pas biaiser la mesure, il faut relever la valeur du CPI dans le fichier stats à la date où l'application se termine (ni avant, ni après).

3. Que constatez vous concernant le temps d'exécution et le CPI ?

C.2. Caches de capacité "normale"

1. Faites varier la taille du cache d'instructions de 4 à 1024 cases par puissance de 2, et notez à chaque fois le CPI et le temps de calcul obtenus. Vous utiliserez comme taille de cache de données NDCACHESET=1024 (cache de 16 kibi octets).
2. Faites varier la taille du cache de données de 1 à 1024 cases par puissance de 2, et notez à chaque fois le CPI et le temps de calcul obtenus. Vous utiliserez comme taille de cache d'instructions NICACHESET=1024 (cache de 16 kibi octets).
3. Pour cette application logicielle, quelles tailles de caches pensez-vous qu'il faille choisir pour obtenir (approximativement) les taux de MISS correspondant aux hypothèses faites plus haut (4% pour le cache instruction et 8% pour le cache de données) ?

C.3. Caches désactivés

Relancez l'exécution du simulateur en désactivant les deux caches, c'est-à-dire en utilisant les valeurs : NICACHESET=0 et NDCACHE =0.

1. Quelle est la durée d'exécution du programme ?
2. Quelle est la valeur du CPI ?

C.4. Représentation graphique

• En reprenant vos résultats de l'exercice C.2., créez un fichier texte dans lequel vous mettrez, à chaque ligne du fichier, le nombre de cases du cache d'instructions et la valeur du CPI que vous avez obtenue pour ce nombre. Le format d'une ligne de ce fichier doit être le suivant :

  [...]
  NB_CASES_ICACHE CPI
  NB_CASES_ICACHE CPI
  NB_CASES_ICACHE CPI
  [...]
  

1. Utilisez l'outil gnuplot pour visualiser la courbe représentant l'évolution du CPI en fonction de la taille du cache d'instructions.
2. Refaites la même opération pour le cache de données, afin de générer la courbe représentant l'évolution du CPI en fonction de la taille du cache de données.