Problème 1001
Un alpiniste possède des grilles dont les cases contiennent des entiers strictement positifs figurant l'altitude des zones d'un massif montagneux.Dans ces grilles, chaque nombre autre que 1 est la somme d'un nombre situé sur la même ligne et d'un nombre situé sur la même colonne que lui. Le plus grand nombre de la grille est le « pic ».
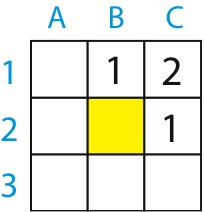
- Complétez la grille de l'alpiniste ci-contre de taille 3 × 3 (un nombre et un seul par case de 1A à 3C) de sorte que la case jaune (2B) contienne le pic le plus grand possible.
- 4A. Quelle est le plus grand pic possible d'une grille 4 × 4 de l'alpiniste ?
L'algorithme écrit pour ce problème effectue une énumération naïve et a un cout qui explose en la taille de la grille puisque le nombre de confgurations à explorer est N! pour N cases. Pour N = 16 (grille 4 × 4), le temps devient relativement prohibitif (16! = 20 922 789 888 000). On peut néanmoins simplement remarquer que le premier chiffre à placer n'a que 3 emplacements différents si l'on tient compte des symétries (une des 4 cases dans un coin, une des 4 cases centrales, ou une des 8 autres cases). Cela diminue le nombre de configurations à explorer à 3 923 023 104 000 (ce qui prend quelques jours). Si l'on veut réduire ce nombre, il faut remarquer qu'il y a nécessairement quatre "1" sur des lignes/colonnes différentes, auquel cas le calcul redevient à nouveau quasiment instantané.
Le programme est ici.
Le programme est ici.
- Le pic maximal de la grille 3 × 3 est 8.
- Le pic maximal d'une grille 4 × 4 est 48.