Problem 1001
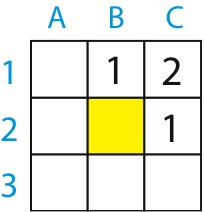
An alpinist has grids whose squares contain strictly positive integers showing the altitude of a massif zones.In this grids, each number different from 1 is the sum of a number located on the same line and of a number located on the same column as itself. The biggest number of the grid is the "peak".
- Complete the following grid of size 3 × 3 (a single number per square from 1A to 3C) so that the yellow square (2B) contains the highest possible peak.
- 4A. What is the highest possible peak of a 4 × 4 alpinist grid?
The algorithm written for this problem does a naive enumeration and has a cost which explodes with the number of squares in the grid, since the number of configurations to explore is N! for N squares. For N = 16 (4 × 4 grid), the times becomes prohibitive (16! = 20 922 789 888 000). We can however notice that the first figure to write only has 3 relevant locations given the symmetries (one of the 4 squares in a corner, one of the 4 central squares, or one of the 8 other squares). This diminishes the number of configuratons to explore to 3 923 023 104 000 (what takes a few days). If we want to reduce this number, we need to notice that there are necessarily four "1" on different lines/columns, in which case the computation time is almost instantaneous.
The program is here.
The program is here.
- The highest peak of the 3 × 3 grid is 8.
- The highest peak for a 4 × 4 grid is 48.