Quentin L. Meunier

Problème 1011

Autour des 25 blocs immobiliers carrés de Cubic-City, les côtés, mesurant tous 1 km, sont des routes à double sens. Un autobus part de A pour aller en B. Il peut passer 2 fois par le même carrefour, mais jamais 2 fois par la même route.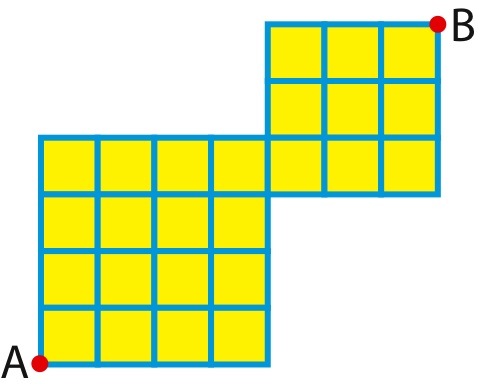

1A. Quelle est le nombre de km du plus long chemin qu'il puisse parcourir entre A et B ?

Deux taxis partent au même moment, l'un de A vers B, l'autre de B vers A. Ils roulent sans arrêt à la vitesse constante de 26 km/h, suivant chacun l'un des chemins les plus courts (13 km). Quand un taxi a le choix entre deux directions, il choisit l'une des deux avec la probabilité 1/2.

2A, 2B. Quelle est la probabilité qu'ils se croisent (à mi-chemin) ?
(le résultat est à donner sous forme de fraction irréductible : son numérateur en 2A et son dénominateur en 2B).

Pour la question 1, le programme suivant effectue une recherche du plus long chemin possible reliant A à B (les arêtes prises sont en blancs et celles non prises en bleu). L'exploration totale prend environ 1 minute (exploration en profondeur avec marquage des cases du tableau correspondant aux arêtes du graphe).

1A. Le plus long chemin de A vers B mesure 51 km.
2A, 2B : La probabilité que deux taxis se croisent est 1/4.