Problem 1011
Around the 25 square blocks of Cubic-City, the sides, measuring 1 km each, are two-way roads. A bus leaves from A to go in B. It can pass 2 times by the same crossroads, but never 2 times by the same road.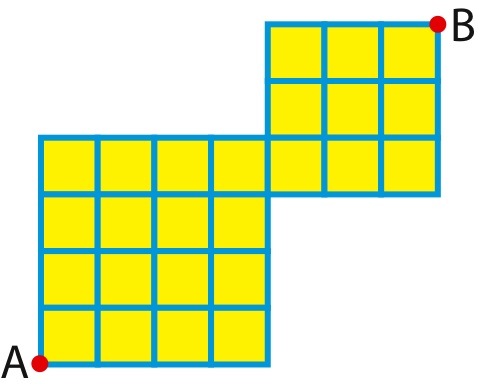
- 1A. What is the number of km of the longest path he can travel between A and B?
Two taxis depart at the same time, one from A to B, the other from B to A. They roll constantly at a constant speed of 26 km/h, following each one of the shortest paths (13 km). When a taxi has the choice between two directions, he chooses one of the two with the probability 1/2.
- 2A, 2B. 2A, 2B. What is the probability that they will intersect (halfway)?
For question 1, the following program makes a search of the longest possible path from A to B (the edges taken are in white, the one not taken are in blue). The total exploration takes around 1 minute (depth first exploration with marking of the elements of the array corresponding to the edges of the graph).
I didn't write a program for question 2.
I didn't write a program for question 2.
- 1A. The longest path from A to B is 51 km long.
- 2A, 2B : The probability that the two taxis intersect is 1/4.