Problème 1012
Le triangle ABC, dangereux pour la navigation, a pour aire 756 km2 et pour côtés des nombres entiers de km (AB mesure 42 km).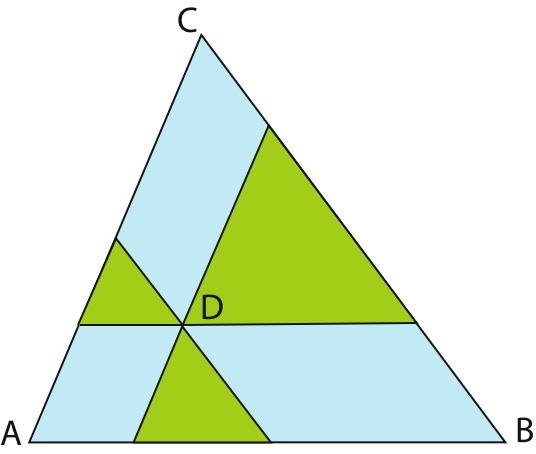
Pour chaque point D où un navire a sombré, une association a tracé une carte où les parallèles aux côtés de ABC passant par D délimitent trois "triangles de recueillement".
Pour le naufrage du Père Dition, le périmètre de chacun de ces triangles est égal à la longueur du côté de ABC avec lequel il possède un côté commun.
- 1A. Quelle est, en mètres, la distance du point de naufrage du Père Dition au côté AB ?
- 2A. Quelle est, en mètres, la distance entre les deux lieux de sinistre ?
Le programme fait pour cette question teste les centres possibles à l'intérieur du triangle selon un pas donné et regarde pour chaque centre possible celui qui respecte le mieux les contraintes. Pour le première question, l'idée était de démarrer avec un pas plutôt gros (0.01) et de refaire les calculs avec un pas plus fin sur la zone autour du minimum trouvé ; en effet, on sent d'après l'énoncé qu'il ne devrait pas trop y avoir de problème à cause d'extremums locaux. Néanmoins, compte tenu du résultat (nombre entier de kilomètres), on trouve directement une erreur nulle. On peut aussi directement prendre un pas inférieur à 0.001 (1 mètre), et faire l'exploration en quelques heures. Le code est disponible ici.
- 1A. La distance de D au côté [AB] est 12 000 m.
- 2A. La distance de D au point G réalisant une somme minimale des aires est 1 000 m.