Problem 1012
The triangle ABC, dangerous for navigation, has an area of 756 km 2 and for sides integer numbers of km (AB is 42 km).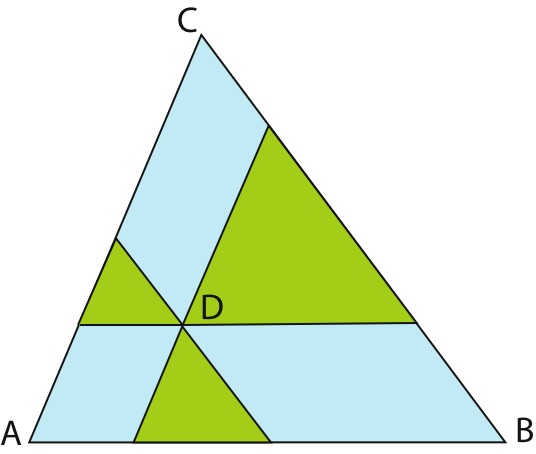
For each point D where a ship sank, an association drew a map where the parallels alongside ABC passing through D delimit three "meditation triangles".
For the sinking of Father "Dition", the perimeter of each of these triangles is equal to the length of the ABC side with which it has a common side.
- 1A. What is, in meters, the distance from the sinking point of Father Dition to the AB side?
- 2A. What is the distance between the two sinking places in meters?
The program made for this question tests the possible centers within the triangle for a given step and looks for each possible center the one that best respects the constraints. For the first question, the idea was to start with a rather big step (0.01) and to redo the calculations with a finer step on the area around the minimum found; indeed, we feel from the statement that there should not be too much trouble because of local extremums. Nevertheless, considering the result (integer number of kilometers), one finds directly a null error. We can also take a step less than 0.001 (1 meter), and make the full exploration in a few hours. The code is available here.
- 1A. The distance from D to the [AB] side is 12 000 m.
- 2A. The distance from D to the point G achieving a minimal sum of the areas is 1 000 m.