Problem 1017

The pizzaiolo makes two perpendicular cuts passing through the same point located 5 cm from the center of a round pizza of 20 cm in diameter.

He gives to Bob two opposite slices (among which the one containing the center), and to Alice the two others. He has chosen the orientation of the cut so that Bob has the greatest possible surface of pizza.

• 1A. How much more pizza will Bob have than Alice? (in cm²)
  
  

The next day, he still gives to Bob and Alice two slices opposed w.r.t. the same summit as the day before. This time, his cuts create four arcs of the same length on the edge of the pizza.

• 2A. How much can Bob have, at most, of pizza more than Alice? (in cm²)
  
  

On the third day, he brings, on a square board, four quarters of the same pizza, wedged at the corners, and offers a quarter of a pizza of 30 cm in diameter, tangent to the four pieces (see drawing).

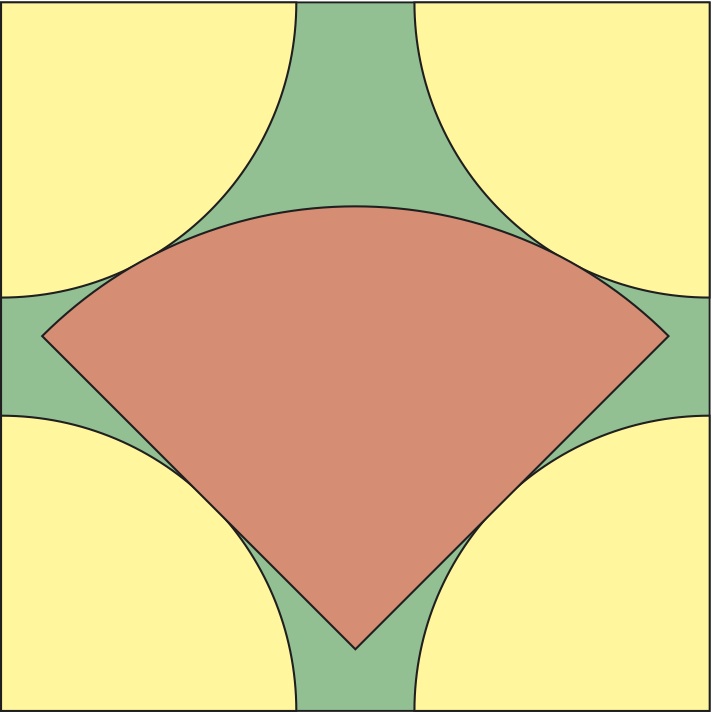
• 3A. What is, in cm², the area of the board?
  
  

(all the results must be rounded to the closest integer).

Note: I haven't done any program for this problem.

See answer