Problème 1022
Le but de ce puzzle est de ranger sans chevauchement sur un « grand carré » quatre pièces identiques en forme de T. Chaque pièce est composée de deux branches rectangulaires, l'une faite de trois petits carrés juxtaposés ayant chacun 50 mm de côté, l'autre d'un nombre N de petits carrés de la même taille dont une extrémité rejoint à angle droit le milieu de la première branche. On appelle la pièce un NT ; le dessin représente un 4T.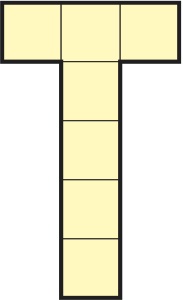
Toutes les réponses seront données en mm et arrondies si besoin à l'entier le plus proche.
- 1A. Quel est, au minimum, la taille d'un côté du grand carré si on peut y placer quatre 1T ?
- 2A. Et si on peut y placer quatre 2T ?
- 3A. Et quatre 3T ?
- 4A. Quel est alors la taille minimale d'un côté de ce grand carré ?
Le programme écrit pour ce problème se limite à l'exploration des grands carrés dans les axes horizontaux et verticaux, et ne considère donc pas par exemple la solution correcte pour la question 3. De même, pour la question 4, le cas N = 7 répond à la question si on ne considère que ces grands carrés, mais pas si l'on considère des grands carrés "penchés". Le programme ne donc la bonne réponse que si l'on démarre à N = 8.
Le principe du programme est de faire une exploration exhaustive pour placer un certain nombre de T donné dans un grand carré. Les 4 positions possibles pour un T sont testées à chaque petit carré de la grille dans son état courant. Si le placement est possible, le T est ajouté à la grille avant l'appel récursif, sinon, l'emplacement suivant est testé.
Le code est disponible ici.
Le principe du programme est de faire une exploration exhaustive pour placer un certain nombre de T donné dans un grand carré. Les 4 positions possibles pour un T sont testées à chaque petit carré de la grille dans son état courant. Si le placement est possible, le T est ajouté à la grille avant l'appel récursif, sinon, l'emplacement suivant est testé.
Le code est disponible ici.
- 1A. 200.
- 2A. 250.
- 3A. 285.
- 4A. 550.