Problem 1022
The purpose of this puzzle is to store without overlap on a "large square" four identical pieces in the shape of T. Each piece is composed of two rectangular branches, one made of three small squares juxtaposed each having 50 mm of side, the other of a number N of small squares of the same size, one end of which joins at right angles the middle of the first branch. This piece is called a NT; the drawing represents a 4T.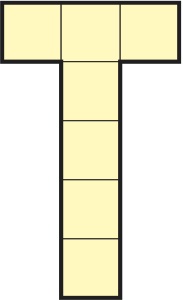
All answers will be given in mm and rounded if necessary to the nearest integer.
- 1A. What is, at least, the size of one side of the big square so that we can place four 1T inside?
- 2A. And with four 2T?
- 3A. And with four 3T?
- 4A. What is then the minimum size of a aide of this big square?
The program written for this problem is limited to the exploration of large squares in the horizontal and vertical axes, and therefore does not consider, for example, the correct solution for question 3. Similarly, for question 4, the case N = 7 answers the question if we consider only these large squares, but not if we consider large squares "leaning". The program therefore only has the correct answer if we start at N = 8.
The principle of the program is to make an exhaustive exploration to place a given number of T's in a large square. The 4 possible positions for a T are tested at each small square of the grid in its current state. If placement is possible, the T is added to the grid before the recursive call, otherwise, the next location is tested.
The code is available here.
The principle of the program is to make an exhaustive exploration to place a given number of T's in a large square. The 4 possible positions for a T are tested at each small square of the grid in its current state. If placement is possible, the T is added to the grid before the recursive call, otherwise, the next location is tested.
The code is available here.
- 1A. 200.
- 2A. 250.
- 3A. 285.
- 4A. 550.