Problème 1026
Un promoteur construit une tour pyramidale formée de trente cubes, tous de même taille, disposés comme ci-contre : seize au premier étage, neuf au deuxième, quatre au troisième et un au quatrième.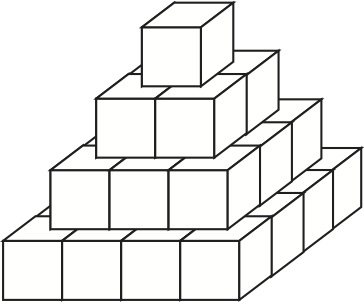
Chaque cube porte un numéro (un entier strictement positif).
À partir du deuxième étage, le numéro d'un cube est égal à la somme des numéros des quatre cubes placés juste au-dessous de lui. Les numéros des cubes du premier étage sont tous différents.
- 1A. Quel est le numéro minimum du cube du quatrième étage ?
Le promoteur souhaite de plus que les numéros des trente cubes soient tous différents.
- 2A. Quel est alors le numéro minimum du cube du quatrième étage ?
Je n'ai pas fait de programme pour ce problème.
- 1A. 352.
- 2A. 365.