Problem 1026

A promoter builds a pyramidal tower formed of thirty cubes, all of the same size, arranged as shown: sixteen on the first floor, nine in the second, four in the third and one in the fourth.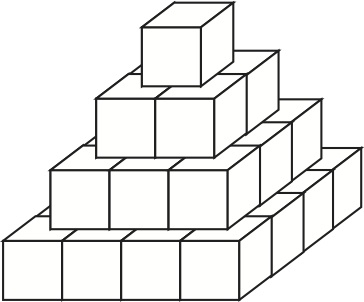


Each cube has a number (a strictly positive integer).
From the second floor, the number of a cube is equal to the sum of the numbers of the four cubes placed just below it. The numbers of the cubes of the first floor are all different.

• 1A. What is the minimum number of the cube of the fourth floor?

The promoter also wants the numbers of the thirty cubes to be all different.

• 2A. What is then the minimum number of the cube of the fourth floor?

See program and comments


See answer